Text Matching: Cosine Similarity

Recently I was working on a project where I have to cluster all the words which have a similar name. For a novice it looks a pretty simple job of using some Fuzzy string matching tools and get this done. However in reality this was a challenge because of multiple reasons starting from pre-processing of the data to clustering the similar words.

Since the data was coming from different customer databases so the same entities are bound to be named & spelled differently. For example: Customer A calling Walmart at Main Street as Walmart#5206 and Customer B calling the same walmart at Main street as Walmart Supercenter. Now you see the challenge of matching these similar text.

After a research for couple of days and comparing results of our POC using all sorts of tools and algorithms out there we found that cosine similarity is the best way to match the text.

What is Cosine Similarity?

From Wikipedia: “Cosine similarity is a measure of similarity between two non-zero vectors of an inner product space that “measures the cosine of the angle between them”

Cosine Similarity tends to determine how similar two words or sentence are, It can be used for Sentiment Analysis, Text Comparison and being used by lot of popular packages out there like word2vec.

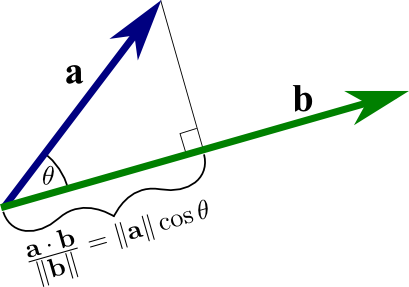
So Cosine Similarity determines the dot product between the vectors of two documents/sentences to find the angle and cosine of that angle to derive the similarity. Here we are not worried by the magnitude of the vectors for each sentence rather we stress on the angle between both the vectors. So if two vectors are parallel to each other then we may say that each of these documents are similar to each other and if they are Orthogonal(An orthogonal matrix is a square matrix whose columns and rows are orthogonal unit vectors) then we call that the documents are independent of each other.

Dot Product: This is also called as Scalar product since the dot product of two vectors gives a scalar result. For example

**Vector(A)** = [5,0,2]
**Vector(B)** = [2,5,0]

Their dot product

**vector(A).vector(B)** = 5_2+0_5+2*0=10+0+0
=10

So the Geometric definition of dot product of two vectors is the dot product of two vectors is equal to the product of their lengths, multiplied by the cosine of the angle between them. So more the documents are similar lesser the angle between them and Cosine of Angle increase as the value of angle decreases since Cos 0 =1 and Cos 90 = 0, You can see higher the angle between the vectors the cosine is tending towards 0 and lesser the angle Cosine tends to 1.

Numerical Feature Vectors

As a first step to calculate the cosine similarity between the documents you need to convert the documents/Sentences/words in a form of feature vector first. There are several methods like Bag of Words and TF-IDF for feature extracction. The most simple and intuitive is BOW which counts the unique words in documents and frequency of each of the words.

Bag of Words(BOW):

Example:

I’m using Scikit learn Countvectorizer which is used to extract the Bag of Words Features:

from sklearn.feature_extraction.text import CountVectorizer
import pandas as pd
count_vect = CountVectorizer()
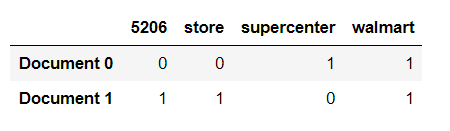
Document1= "Walmart Supercenter"
Document2= "Walmart Store 5206"

corpus = [Document1,Document2]

X_train_counts = count_vect.fit_transform(corpus)

pd.DataFrame(X_train_counts.toarray(),columns=count_vect.get_feature_names(),index=['Document 0','Document 1'])

Here you can see the Bag of Words vectors tokenize all the words and puts the frequency in front of the word in Document.

Shortcoming of BOW:

The major issue with Bag of Words Model is that the words with higher frequency dominates in the document, which may not be much relevant to the other words in the document. So another approach tf-idf is much better because it rescales the frequency of the word with the numer of times it appears in all the documents and the words like the, that which are frequent have lesser score and being penalized.

TF-IDF:

We will see how tf-idf score of a word to rank it’s importance is calculated in a document

tfidf score of a word w:

tf(w)*idf(w)

Where, tf(w) = Number of times the word appears in a document/Total number of words in the document

idf(w) = Number of documents/Number of documents that contains word w

from sklearn.feature_extraction.text import TfidfVectorizer
vectorizer = TfidfVectorizer()
trsfm=vectorizer.fit_transform(corpus)
pd.DataFrame(trsfm.toarray(),columns=vectorizer.get_feature_names(),index=['Document 0','Document 1'])

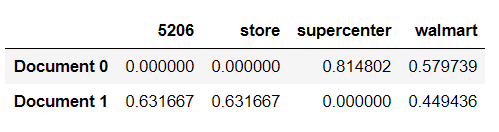
Here you can see the tf-idf numerical vectors contains the score of each of the words in the document.

So far we have learnt what is cosine similarity and how to convert the documents into numerical features using BOW and TF-IDF.

Next we would see how to perform cosine similarity with an example:

We will use Scikit learn Cosine Similarity function to compare the first document i.e. Document 0 with the other Documents in Corpus.

from sklearn.metrics.pairwise import cosine_similarity
cosine_similarity(trsfm[0:1], trsfm)

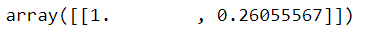
Here the results shows an array with the Cosine Similarities of the document 0 compared with other documents in the corpus. So you can see the first element in array is 1 which means Document 0 is compared with Document 0 and second element 0.2605 where Document 0 is compared with Document 1.