Reshaping numpy arrays in python
Reshape is an important feature which lets you to change the shape of your array without changing its data
whereas ravel is used to get the 1D contiguous flattened array containing the input elements
In this post we will see how ravel and reshape works and how it can be applied on a multidimensional array
Additionally we will also learn array indexing and order difference between C and Fortran
What is Reshaping?Permalink
It is defined as changing the shape of an array. For example an One dimensional array can be changed to a 2x3 Matrix and a multi-dimensional array 2x3 can be reshaped to 6x2

Contiguous arrayPermalink
Before jumping to numpy.reshape() we have to understand how these arrays are stored in the memory and what is a contiguous and non-contiguous arrays
A contiguous array is just an array stored in an unbroken block of memory and to access the next value in the array, we just move to the next memory address
Consider the 2D array arr = np.arange(12).reshape(3,4). It looks like this:
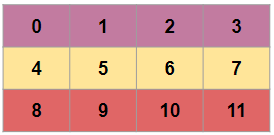
In a computer memory this is stored as

This is also known as row-major order methods for storing multidimensional arrays in linear storage such as random access memory.

image source: wikipedia
It is also called as C Contiguous layout (order ‘C’) because C arrays always start at zero and stored as contiguous block of memory
So the next memory address holds the next row value on that row.
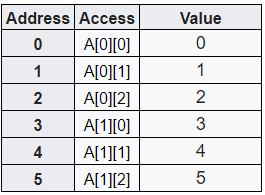
The array arr elements in C arrays are row major order as shown in this table
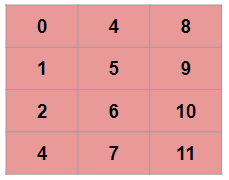
Fortran Contiguous or Column major
if you transpose the above array then it becomes Fortran contiguous layout i.e. order ‘F’
arr.T
By default Fortran arrays start at 1 and also known as column-major order methods for storing multidimensional arrays in linear storage such as RAM
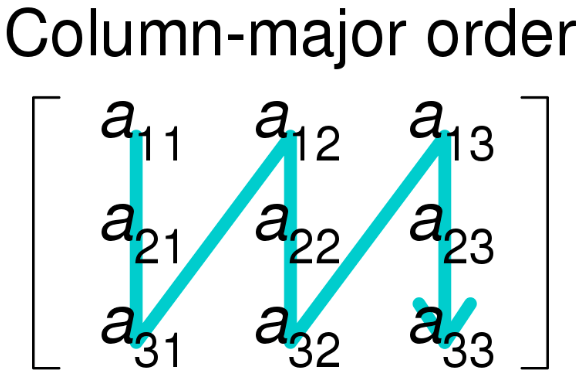
image source: wikipedia
The array arr elements in F contiguous arrays are column major order as shown in below table
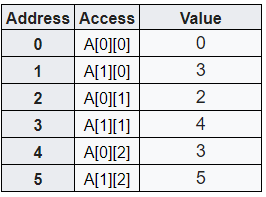
The C contiguous memory layout, row-wise operations are usually faster than column-wise operations
Similarly column wise operation is faster for F contiguous array
So we have understood what is conguous array and what is order difference between C and Fortran(F) and now we can explore numpy.ravel() and numpy.reshape()
It’s important to understand ravel function before jumping to numpy.reshape()
numpy ravel explainedPermalink
numpy.ravel(a, order=’C’)
It returns a contiguous flattened array.
Therefore a 1-D array containing input array elements is returned
Parameters:
a: input array
order = {‘C’,’F’, ‘A’, ‘K’}, optional and by default it is ‘C’
We have order type ‘C’ and ‘F’ in above section.
‘A’ means to read the elements in Fortran-like index order if a is Fortran contiguous in memory, C-like order otherwise
and ‘K’ means to read the elements in the order they occur in memory
Let’s understand the ravel function with the help of an example
Create an Array
x = np.array([[1, 2, 3], [4, 5, 6]])
array([[1, 2, 3],
[4, 5, 6]])
numpy ravel with order CPermalink
Now we will apply ravel() function to this array x with default order type ‘C’
np.ravel(x)
array([1, 2, 3, 4, 5, 6])
Because the order is C contiguous i.e. row major as explained in above section the output is same as array stored in the memory block for C contiguous array
numpy ravel with order FPermalink
Now apply the nump.ravel() function to same array and this time order is set as F contiguous
np.ravel(x, order='F')
array([1, 4, 2, 5, 3, 6])
So the order is F i.e. column major therefore the output is same as value stored in memory for F contiguous
numpy ravel with order APermalink
Let’s transpose the original array x to get a F contiguous array and then apply ravel function to it
np.ravel(x.T)
array([1, 4, 2, 5, 3, 6])
So the output is same as ravel with order F above
Next we will pass the order as ‘A’ in this ravel function
np.ravel(x.T,order='A')
array([1, 2, 3, 4, 5, 6])
So the output is same as order with ‘C’ because we passed order ‘A’ and original array x is C-like order so it remains same even after it’s Transposed
numpy.reshape()Permalink
numpy.reshape(a, newshape, order=’C’)
This function gives a new shape to the input array and without changing the data
parameters:
a: input array
newshape: new desired shape of the array which should be compatible with the original shape. and if given -1 then the value is inferred from the length of array
order = {‘C’,’F’, ‘A’, ‘K’}, optional and by default it is ‘C’
Now reshaping is like raveling the input array and then inserting the elements from the raveled array into the new array

Let’s understand this with the help of some code
Create an Array
x = np.array([[1, 2, 3], [4, 5, 6]])
array([[1, 2, 3],
[4, 5, 6]])
This a 2x3 array and we want to reshape it to 3x2
np.reshape(x,(3,2))
array([[1, 2],
[3, 4],
[5, 6]])
Let’s pass the ravelled x into the reshape function and see what happens
np.reshape(np.ravel(x),(3,2))
array([[1, 2],
[3, 4],
[5, 6]])
So the output is same as the previous output because as explained above reshaping is like ravelling the data first and then reshaping it
newshape dimension as -1
np.reshape(np.ravel(x),(3,-1))
array([[1, 2],
[3, 4],
[5, 6]])
The output is same here as previous one with shape (3,2) because when dimension -1 is given then it infers the value as 2 based on original shape of array
numpy reshape 1D to 2DPermalink
create a 1D array
A = np.array([1,2,3,4,5,6])
array([1, 2, 3, 4, 5, 6])
convert 1D array to 2D using reshape
np.reshape(A,(3,2))
array([[1, 2],
[3, 4],
[5, 6]])
ConclusionPermalink
In this post you’ve learnt about numpy reshape and ravel functions
You now know:
- C Contiguous and F contiguous array layout and their differences
- How is memory stored for multidimensional arrays
- ravel function returns a 1D array given a multi-dimensional array as input
- How reshape works with ravel
- Column major and row major methods of storing multi-dimensional arrays
How you are using numpy in your work or projects? If you’re just learning about them, then how do you plan to use them in the future?
Do share your experience using ravel and reshape functions and Let me know in the comments below!