How to create bins in pandas using cut and qcut

Data Binning

It’s a data pre-processing strategy to understand how the original data values fall into the bins. For example: In some scenarios you would be more interested to know the Age range than actual age or Profit Margin than actual Profit

Histograms are example of data binning that helps to visualize your data distribution in equal intervals

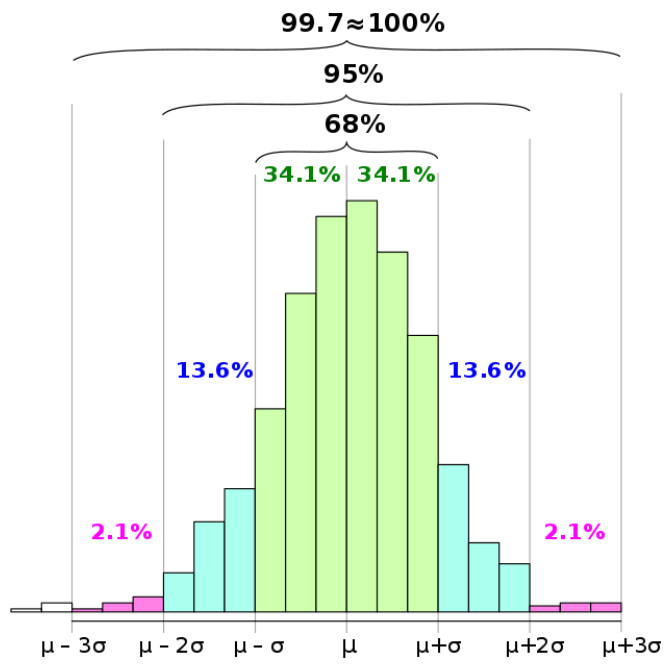
Look at this 68–95–99.7 rule empirical rule for normally distributed data. This tells the percentage of data in each of the following bins around the means

[Mean-SD, Mean+SD] 68%
[Mean-2SD, Mean+2SD] 95%
[Mean-3SD, Mean+3SD] 99.7%

Pandas Cut

In this post we are going to see how Pandas helps to create the data bins using cut function

pandas.cut(x, bins, right: bool = True, labels=None, retbins: bool = False, precision: int = 3, include_lowest: bool = False, duplicates: str = ‘raise’)

Do not get scared with so many parameters we are going to discuss them later in the post

First parameter x is an One Dimensional array that needs to be binned

Creating Data for Binning

We will create the Sales figure of a Company for two years i.e. from 1-JAN-2018 thru 31-Dec-2019

import numpy as np
import pandas as pd
arr = np.random.randint(1,10000,24)
df = pd.DataFrame({'Sales':arr},index=pd.date_range(start='1/1/2018', periods=24,freq='MS'))

Pandas Cut Custom Bins

Let’s divide the above sales figures for 24 months into 4 equal size bins i.e. [0, 2500, 5000, 7500, 10000]

Why we have taken bins between 0 and 10,000? Because our sales figure above is created using random integer between 1 and 10K

df['Sales_Bins']=pd.cut(df.Sales,bins = [0,2500,5000,7500,10000])
df.head()

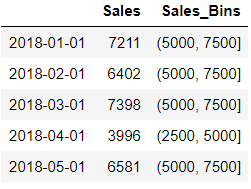
We added the respective bin values for sales in a new column Sales_Bins

Let’s count that how many months out of 24 falls into each bins

df['Sales_Bins'].value_counts().sort_index()
(0, 2500]         2
(2500, 5000]      8
(5000, 7500]     12
(7500, 10000]     2
Name: Sales_Bins, dtype: int64

We can see that the most of sales happens between 5000 and 7500

Label the bins

We should get the original dataframe back first. So we will drop the extra column Sales_bins for labelling

df.drop(['Sales_Bins'],inplace=True,axis=1)

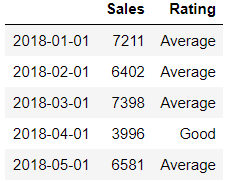
Now we want to label these Sales values as Fair, Good, Better, Excellent based on the bins

**0, 2500 Fair
2500, 5000 Good
5000, 7500 Better
7500, 10000 Best**

We will pass an additional parameter labels containing array of labels

The labels will be added to a new column called Rating

df['Rating']=pd.cut(df.Sales,bins = [0,2500,5000,7500,10000],labels=['Fair','Good','Average','Best'])
df.head()

Interval Index - Create Equally Spaced Bins

So far we have seen how we can create bins of the data by passing array of bins

Now instead of array we can also pass the IntervalIndex i.e. An interval of Index which are closed on same side

Interval Index is constructed using pandas.Interval_Range

pandas.interval_range(start=None, end=None, periods=None, freq=None, name=None, closed=’right’)

If we want to create Interval index for Sales figure above i.e. 4 equally spaced bins

pd.interval_range(start=0, end= 10000, periods=4)

IntervalIndex([(0, 2500], (2500, 5000], (5000, 7500], (7500, 10000]],
              closed='right',
              dtype='interval[int64]')

Voila !! it has created those 4 bins that we used above

Let’s pass this Interval Index in the bins and check if we get the same results

We are dropping the Rating column first and then passing IntervalIndex with start value as 0 and end value as 10000 and periods is set to 4

df.drop(['Rating'],inplace=True,axis=1)
df['Sales_Bins']=pd.cut(df.Sales,bins = pd.interval_range(start=0, end= 10000, periods=4))
df.head()

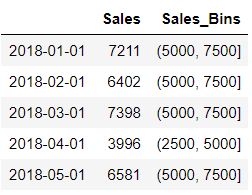
Understanding Intervals

Did you observe those bins or intervals and the bracket which is not consistent ?

Isn’t it Strange that those bin values are having a Round Brackets at the start and Square brackets at the end. for example: (5000, 7500]

It basically means any value on the side of round bracket is not included in the bin and any value on the side of square bracket is included

In Mathematics, this is called as open and closed intervals. if we have round brackets on both sides then it’s an open interval and square on both sides is closed intervals

so in our case (5000,7500] value of 5000 is not included in this bin but a value of 7500 is included

You can control this while creating the IntervalIndex using interval_rang Closed parameter which can take any of these values

{‘left’, ‘right’, ‘both’, ‘neither’}, default ‘right’

Include Lowest Parameter

if you want to include the first interval then this should be set to True. By default it is set to False

Let’s understand this with the help of an example. We will take our Sales dataframe

Create a dataframe sorted by Sales column and with a dateIndex ranging from 2018/1/1/ to 2019/11/01

import numpy as np
import pandas as pd
arr = np.random.randint(1,10000,23)
df = pd.DataFrame({'Sales':arr},index=pd.date_range(start='1/1/2018', periods=23,freq='MS'))
df.sort_values('Sales',ascending=True,inplace=True)

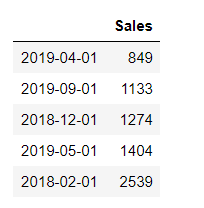
We will create a custom bin that includes the lowest Sales value as first interval

bins = [ 849, 2500, 5000, 7500, 10000]

Create these bins for the sales values in a separate column now

pd.cut(df.Sales,retbins=True,bins = [108,5000,10000])

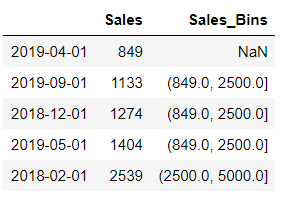
There is a NaN for the first value because that is the first interval for the bin and by default it is not inclusive

Add a new parameter include_lowest and set it to true and check the result

df['Sales_Bins']=pd.cut(df.Sales,bins = [ 849, 2500, 5000, 7500, 10000],include_lowest=True)
df.head()

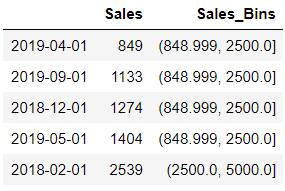
Return Bins

This parameter if set to True will returns the bins and is useful when bin is passed as a Single Scalar value

Let’s understand with our Original Sales example

We will set the bins value as 4 this time i.e. No arrays or No IntervalIndex

It returns the bins value also along with the results

df.drop(['Sales_Bins'],inplace=True,axis=1)
result, bins=pd.cut(df.Sales,retbins=True,bins = 4)
print(bins)

array([ 264.408, 2672. , 5070. , 7468. , 9866. ])

So these are the four bins used [(264.408, 2672] , (2672, 5070], (5070, 7468], (7468, 9866]]

Pandas qcut

qcut is a quantile based function to create bins

Quantile is to divide the data into equal number of subgroups or probability distributions of equal probability into continuous interval

For example: Sort the Array of data and pick the middle item and that will give you 50th Percentile or Middle Quantile

Lets’ understand this with Sales example used above. Use the describe function on Sales column

 df.Sales.describe()

count      23.000000
mean     4510.173913
std      2578.658295
min       849.000000
25%      2851.000000
50%      4065.000000
75%      6208.000000
max      9860.000000
Name: Sales, dtype: float64

Here Min value is 0th percentile and 25% is the 25th Percentile and so on or In other words you can say 0th quantile and 0.25th quantile

Let’s use the Numpy Quantile function and see if we get the same result as above

We will use the following values to determine the Min(0), 0.25, 0.5, 0.75 and Max(1) quantile value of this data

import numpy as np
np.quantile(df.Sales,[0,0.25,0.5,0.75,1])

array([ 849., 2851., 4065., 6208., 9860.])

We will use qcut to create 4 equally sized bins i.e quartiles

df['Sales_Bins'] = pd.qcut(df.Sales,4)
df.Sales_Bins.value_counts().sort_index()

(848.999, 2851.0]    6
(2851.0, 4065.0]     6
(4065.0, 6208.0]     5
(6208.```0, 9860.0]     6
Name: Sales_Bins, dtype: int64

Look at these Bins values that is exactly same as what we derived from the numpy quantile function

Let’s Try with Octiles

So 8 quantiles are called Octiles and if we divide 1 into 8 equal parts then we will get these values

[0, 0.125, 0.25, 0.375, 0.5, 0.625, 0.75, 0.875, 1]

First Calculate these Octiles value using numpy

import numpy as np
np.quantile(df.Sales,[0, 0.125, 0.25, 0.375, 0.5, 0.625, 0.75, 0.875, 1])

array([ 849. , 1371.5 , 2851. , 3395.5 , 4065. , 4889.75, 6208. ,8109.75, 9860. ])

Let’s find the Octile bins for our sales data and generate 8 equally sized bins using qcut. You can either pass the entire list to qcut or just pass a q value of 8. In both the cases result would be same

We are also using labels parameter here to show those Sales value falls in which bin out of eight quantiles

df['Sales_Bins'] = pd.qcut(df.Sales,q=8,labels=['1st','2nd','3rd','4th','5th','6th','7th','8th'])
df.head(10)

Let’s get those bin intervals using retbins and see if these intervals are exactly matching with the Octile output computed using numpy above

df['Sales_Bins'],bins = pd.qcut(df.Sales,q=8,labels=['1st','2nd','3rd','4th','5th','6th','7th','8th'],retbins=True)
bins

array([ 849. , 1371.5 , 2851. , 3395.5 , 4065. , 4889.75, 6208. , 8109.75, 9860. ])

e by now you will have a better understanding how qcut works and how it is different from the cut function

I am not discussing other parameters for qcut like retbins because rest of the parameters for qcut will be same as pandas cut as shown in the first part of this post

Conclusion

Here are the keys points to summarize that we learnt and discussed so far in this post

• Pandas Cut function can be used for data binning and finding the data distribution in custom intervals
• Cut can also be used to label the bins into specified categories and generate frequency of each of these categories that is useful to understand how your data is spread
• IntervalIndex is one of the parameters that will give the range of values and timestamps to generate equally sized bins using pandas Interval_Range
• By default the lowest interval of the bin is not inclusive so you have to set the include_lowest as True explicitly
• Cut and qcut function also returns the bins value (ndarray of floats) along with the output
• qcut function can be used to generate equally sized quantiles bins for your data
• Finally we have seen how qcut work with octiles on Sales data and generating the quantiles using numpy

---