Find nearest neighbor using KD Tree
KD Tree is a modified Binary Search Tree(BST) that can perform search in multi-dimensions and that’s why K-dimensional.
The KD tree differs from the BST because every leaf node is a k-dimensional point here.
Before you think what a dimension means here, Let me tell you that in a vector of 5 elements it is referred to as 5 dimensions.
For example, A 5-dimensional record of an employee will look like this: [EmplID. Age, Salary, Year of Exp, distance from home to office]
What is a Discriminator?
There is a discriminator for each node that ranges from 0 to k-1 (inclusive) that makes branching decisions based on a particular search key associated with that level
All node have same discriminator at any level. So the root node will have discriminator 0 and it’s two child nodes will have discriminator 1 and so on
How to Build a KD Tree?
In the 2-Dimensional case each point has two values it’s x and y coordinates. So we will first split on the x-coordinate, next on y-coordinate and then again on x-coordinate and so on
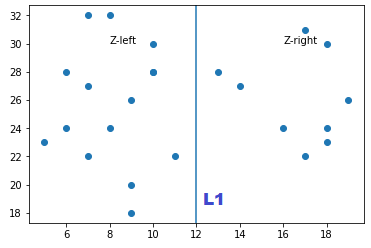
Let’s assume we have set of points like this Z = [(2,19),(3,5),(6,8),(7,9)…..] in a 2-dimensional plane. At the root node it will be split on the x-coordinate first so all points having x<12 will be on the left and points having x>12 is on the right
Let’s call the subset of points to the left of splitting line as Z-left and subset of points to the right of splitting line as Zright
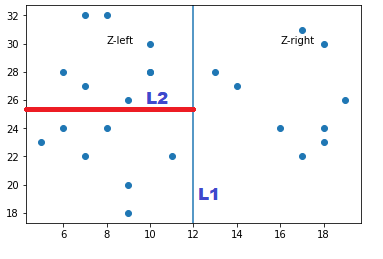
Now take the Z-left subset and split it Horizontally with a splitting line L2. Similarly we will split the right subset of points with a horizontal line and the two subsets are horizontally split into two another subset
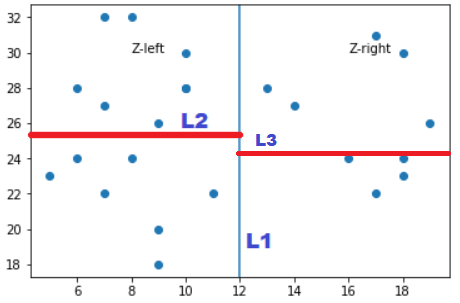
Now this newly formed subsets by L2 and L3 will be split again by Vertical splitting line, So we are splitting a node with vertical line whose depth is even and splitting a node with horizontal line whose depth is odd
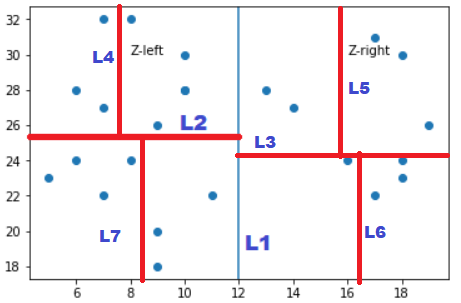
Now you would be having a question like how to decide if we have to split horizontally or vertically? If we create a recursive function to create the KD Tree then a user has to pass two parameters to this function first the input Array of K-dimensional points and the depth of the KD Tree to determine whether we must split with a vertical or a horizontal line
The splitting lines are inserted by selecting the median, with respect to their coordinates in the axis being used to create the splitting plane.
A kd-tree for a set of n points uses O(n) storage and can be constructed in O(n logn) time
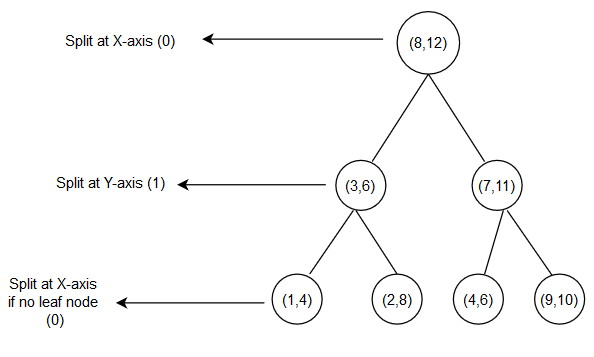
Here is the final K-D Tree will look like
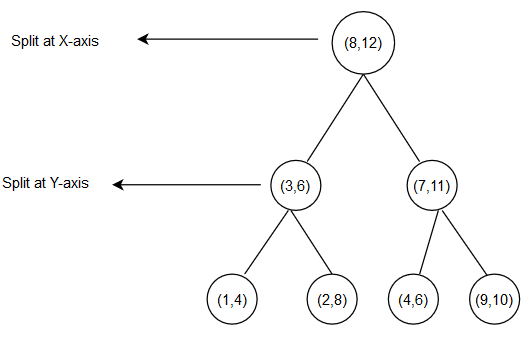
Output of KD Tree would look like this:
((8, 12),
((3, 6), ((1, 4), None, None), ((2, 8), None, None)),
((7, 11), ((4, 6), None, None), ((9, 10), None, None)))
Attributes for building K-D Tree
Here are three main points that needs to be taken care for building a K-D Tree:
- What dimension to split? Choose the Widest dimension first or the alternating dimensions
- What value to split? Choose the median value or the Centre of all the values
- When do we stop splitting? When there are fewer data points are left than a specific value say m
How Nearest Neighbor Search Query works in a K-D Tree?
Before we start we must understand what are the values that are stored at each node to build an intuitive data structure like K-D Tree
We will basically store following three information at each node:
-
Axis X or Y used for splitting?
-
Split value
-
Bounding Box - It is the smallest box that contains all the points within that node.
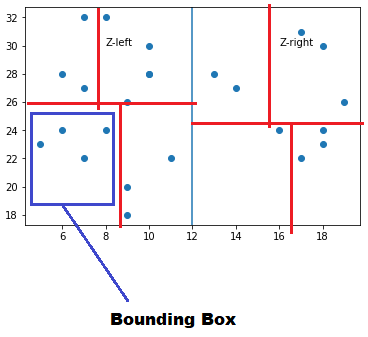
Steps to follow for Query Search:
The path traversed to reach Query point A(2,8) satisfies all the splitting conditions down the tree at each node to this point and we will continue searching until a leaf node is reached
-
Start from the root node and moves recursively in the same way as it is build. The x value of Query point A(2,8) is compared with that of Z (8,12) to determine in which direction to branch. Because A x’s value is less than P’s x value, we branch to the left subtree
-
At root level we really don’t care about the Query point A y’s value and it’s doesn’t affect the decision on which way to branch at root level
-
At the second level it is Query point A y’s value is compared with the node (3,10) y’s value i.e. 8 is greater than 6 so we will branch to the right subtree
-
Compare the Node value (2,8) with A(2,8), Is it same? Yes, then Stop
-
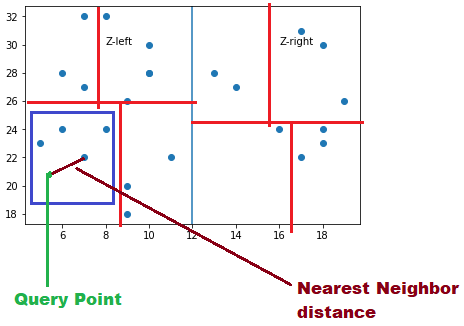
Compute the distance of each point contained in the bounding box to the Query point A
-
Can a nearest neighbor necessarily be inside the bounding box? Not really, it can live in another box also. There can be another points closer in adjacent boxes
-
So what we will do find other points in adjacent boxes that can be nearest compared to the nearest one in the same box. We will traverse backward and start finding the distance with the other points in neighboring boxes
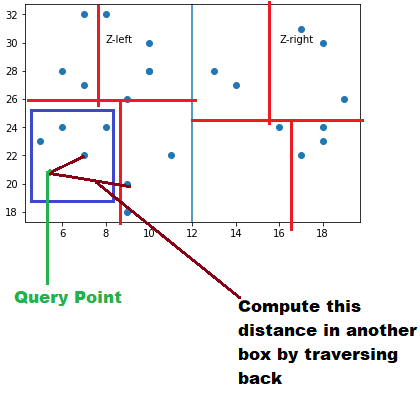
-
Compute the distance between Query point and all the points in neighboring box. And we will say that a new nearest neighbor is found in the adjacent box which is smaller than the nearest neighbor point in the same box found in Step 5
-
As a final step, We will traverse backward to the previous node and check if the distance to that bounding box is less than the new nearest neighbor found in step 8 or not
distance to bounding box for a node < distance to the nearest neighbor -
Prune all the nodes where the distance of bounding box is greater than the nearest neighbor and that way you don’t have to compute the distance with each point inside that box
-
After pruning all such boxes whatever is left will give the nearest neighbor based on their distance from the query point. so if query is to find two nearest neighbor then first neighbor is point found in step 8 and second nearest neighbor is point found in step 5
-
KD Tree in Sklearn
Let’s see how KD Tree works using scikit-learn, We will take a list of 2 dimensional points
Z = [(5,23),(6,28),(8,24),(10,28),(9,26),(10,30),(7,22),(9,18),
(6,24),(8,32),(9,20),(7,32),(7,27),(18,30),(11,22),(17,31),
(13,28),(16,24),(19,26),(10,28),(14,27),(18,23),(17,22),(18,24)]
Sklearn has a NearestNeigbors class that uses various algorithms for implementing neigbor searches. One of the Algorithm in that list is KD Tree. The other algorithms are out of score for this post
from sklearn.neighbors import NearestNeighbors
neigh = NearestNeighbors(n_neighbors=2, radius=0.4, algorithm = 'kd_tree')
Let’s take a query point (10,28) and find out the 3 nearest neighbor to this point
>> neigh.kneighbors([[10,28]], 3, return_distance=False)
array([[ 3, 19, 5]], dtype=int64)
This returns an array of Indexes of the 3 points nearest to the Query point. Let’s checkout those three points
>> [Z[y] for (x,y) in np.ndenumerate(idxs)]
[(10, 28), (10, 28), (10, 30)]
There are other methods like radius_neighbors that can be used to find the neighbors within a given radius of a query point or points
KD Tree in Scipy to find nearest neighbors of Geo-Coordinates
Scipy has a scipy.spatial.kdtree class for KD Tree quick lookup and it provides an index into a set of k-D points which can be used to rapidly look up the nearest neighbors of any point
We will take a list of Lat&Long Geo-Coordinates of top metropolitan cities in India and will try to find out the nearest cities to the Query city using KD Tree
Here is the list of few Big cities in India namely: Mumbai, Pune, Bangalore, Indore, Delhi, Gurugram, and Chennai
Z=[(19.076,72.877),(18.52,73.85),(12.97,77.59),(22.71,75.85),(28.704,77.10),(28.45,77.026),(13.0827,80.27)]
Let’s use the Query City as Mumbai and find the 2 nearest neighbor for this city
from scipy import spatial
tree = spatial.KDTree(Z)
The coordinate for Mumbai is (19.076,72.877) i.e. Z[0]. We will use the query function to query the 3 nearest neighboring city to Mumbai from the given list
>> idxs = tree.query(Z[6], 7)
(array([51.82517636, 52.61665991, 55.16873209]), array([0, 1, 2]))
So it returns the distance of those three cities in an ascending order and the index of the cities in the same order of distance.
This distance is the Euclidean distance and not the exact Miles or KM distance between the two cities. You can use Haversine distance or read this article to explore different ways to calculate the distance between the cities.
Let’s checkout what are those 3 cities and in what order the result is displayed
>> [Z_name_list[idx] for idx in idxs[1]]
['Mumbai', 'Pune', 'Indore']
So it perfectly gives all the three neighboring cities to Mumbai. Infact one of the city is Mumbai itself. We should lookup for 4 cities then it will give 3 cities excluding Mumbai
Let’s take another example where we want to find the distance of all these cities from the National Capital Delhi
>> idxs = tree.query(Z[6], len(Z))
(array([ 0. , 0.26456001, 6.12295158, 10.51342537, 10.69001197,
15.74162812, 15.93969616]), array([4, 5, 3, 0, 1, 2, 6]))
>> [Z_name_list[idx] for idx in idxs[1]]
['Delhi', 'Gurugram', 'Indore', 'Mumbai', 'Pune', 'Bangalore', 'Chennai']
Ok so we get all the cities in increasing order by distance from the National Capital Delhi. Hope people who knows about India will find this list as accurate
Since we are looking at the Geo distances in this example, So I wanted to point out that there is a DBSCAN class that Perform DBSCAN clustering from vector array or distance matrix and uses KD Tree as one of the algorithm to find the Clusters within a list of Lat, Longs and to find the geo points within those clusters and a specified radius